L' equazione di una retta passante per due punti distinti (x1,y1) ( x 1, y 1) e (x2,y2) ( x 2, y 2) del piano può essere trovata utilizzando la formula seguente: y −y1 y2 − y1 = x− x1 x2 − x1 y − y 1 y 2 − y 1 = x − x 1 x 2 − x 1. Questa formula è anche detta " condizione di allineamento della retta ". Permette di ottenere l.. Calcolatore gratuito della retta passante per due punti - trova l'equazione di una retta passante per due punti passo dopo passo

Equazione Retta passante per 2 punti Esercizio 1 YouTube

Retta passante per 2 punti formula di interpolazione lineare YouTube
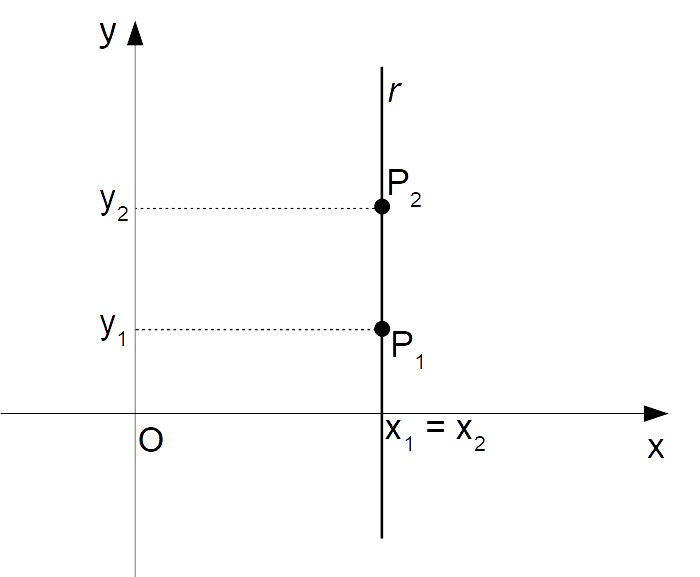
Retta passante per due punti SìMatematica

L'equazione della retta nel piano cartesiano YouTube

Equazione della retta per due punti YouTube

RETTA PARALLELA a un'altra e passante per un PUNTO _ PC69 YouTube
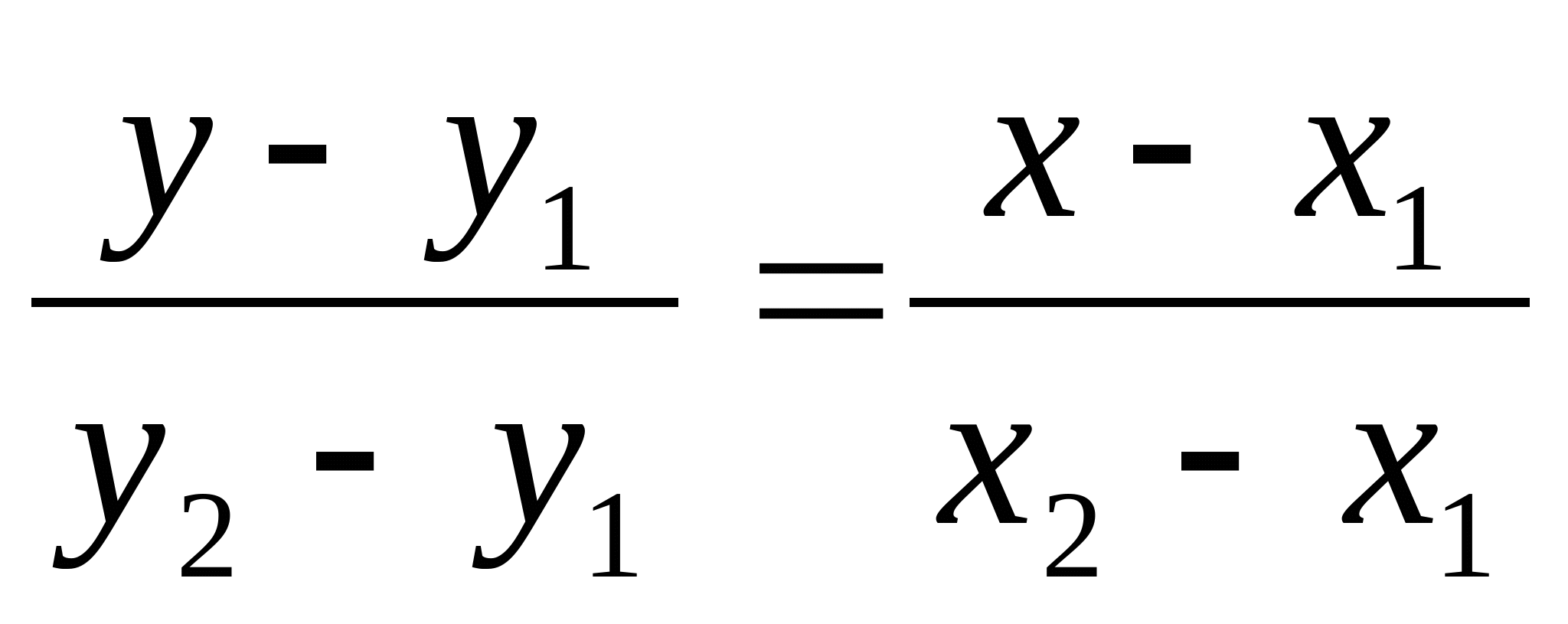
RETTA PASSANTE PER DUE PUNTI Qual è lo

Il Coefficiente Angolare di una Retta dati Due suoi Punti di Passaggio YouTube

Equazione di una retta per due punti. Matematica terza media

Equazione di una Circonferenza dati 2 Punti e la Retta su cui giace il Centro (Metodo Analitico

Retta passante per due punti e suo coeff. angolare YouTube
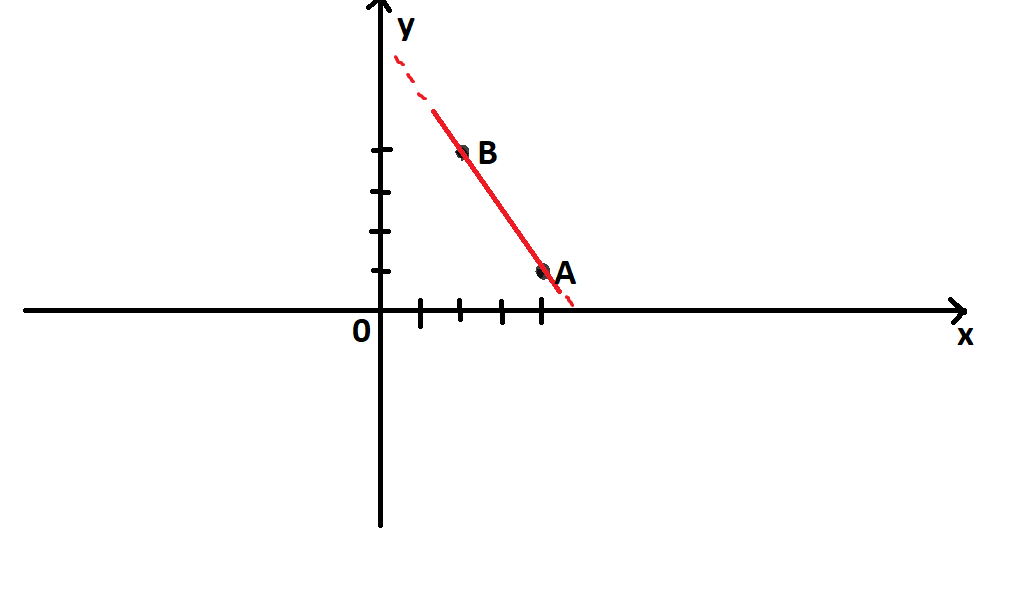
L'Equazione di una retta passante per due punti Blog didattico

Equazione della retta passante per un punto matematicaoggi

1_Equazione della retta passante per un punto e perpendicolare ad un retta data YouTube
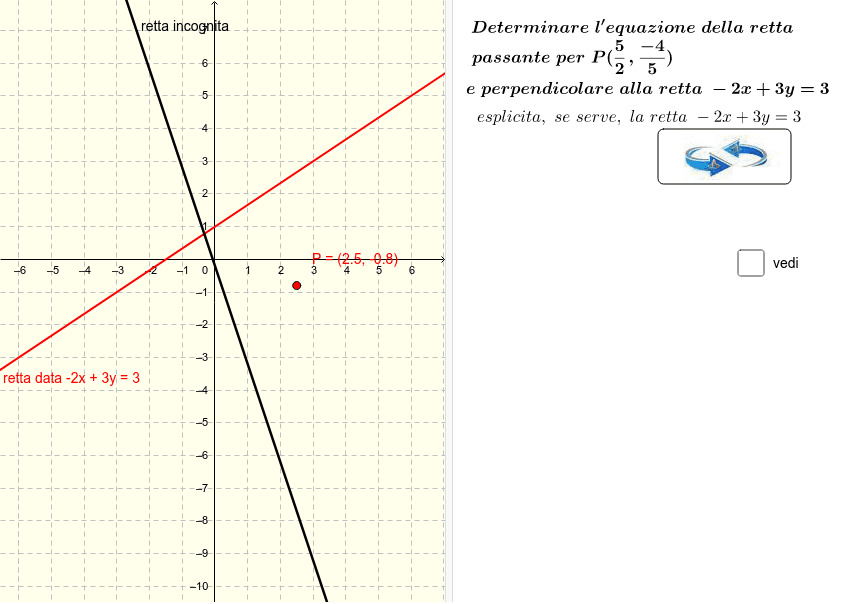
Retta passante per un punto e perpendicolare a una retta GeoGebra

RETTA PERPENDICOLARE a un'altra e passante per un PUNTO _ PC77 YouTube

La retta passante per uno e due punti Andrea il Matematico
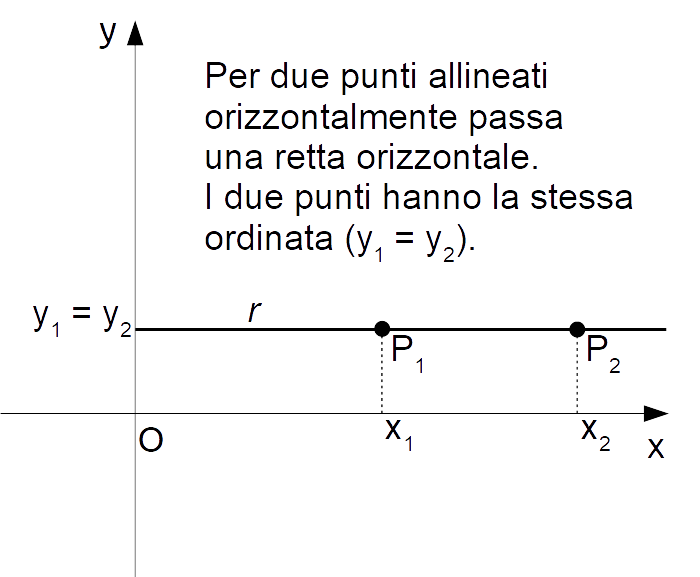
Retta passante per due punti SìMatematica

Equazione Della Retta Passante Per Un Punto ignayler
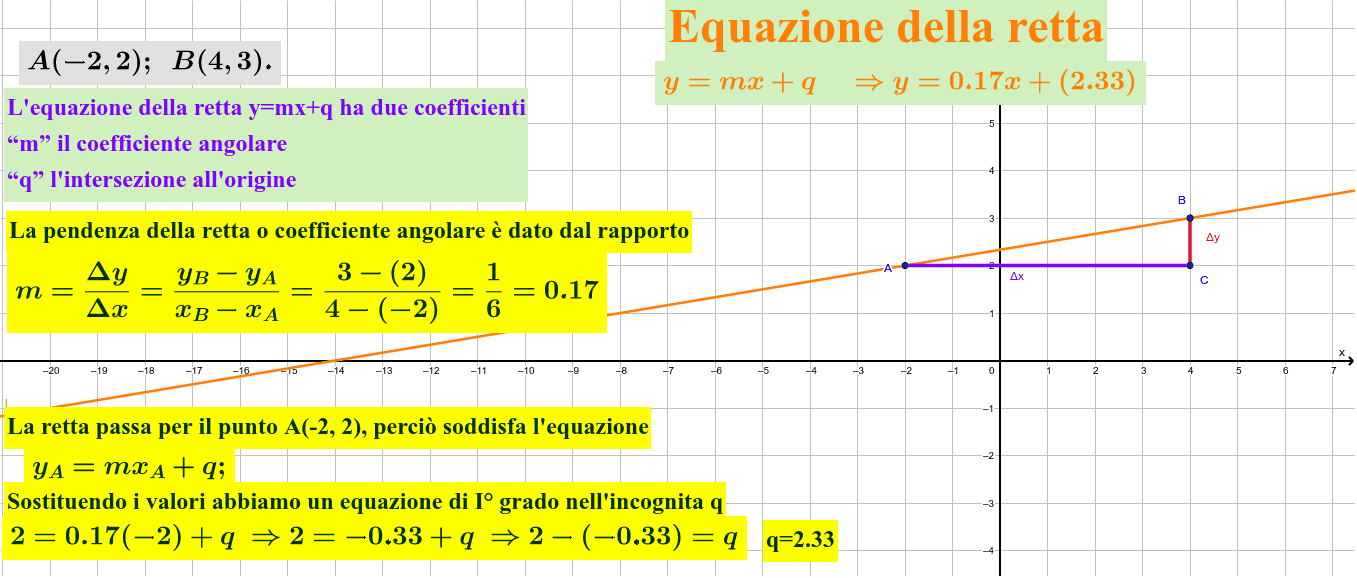
Equazione della retta passante per due punti GeoGebra
Dimostrazione della formula della retta passante per due punti.Playlist classe prime https://www.youtube.com/playlist?list=PLaBGTitzYaOAhzfRqsx2SIcieDoiRCDlJ.. Geometria. Geometria Analitica. La retta passante per due punti ha equazione (x-x 1 )/ (x 2 -x 1 )= (y-y 1 )/ (y 2 -y 1) se i punti considerati non sono allineati né orizzontalmente, né verticalmente. La formula permette quindi di calcolare l'equazione di una retta a partire dalle coordinate cartesiane di due punti appartenenti ad essa.