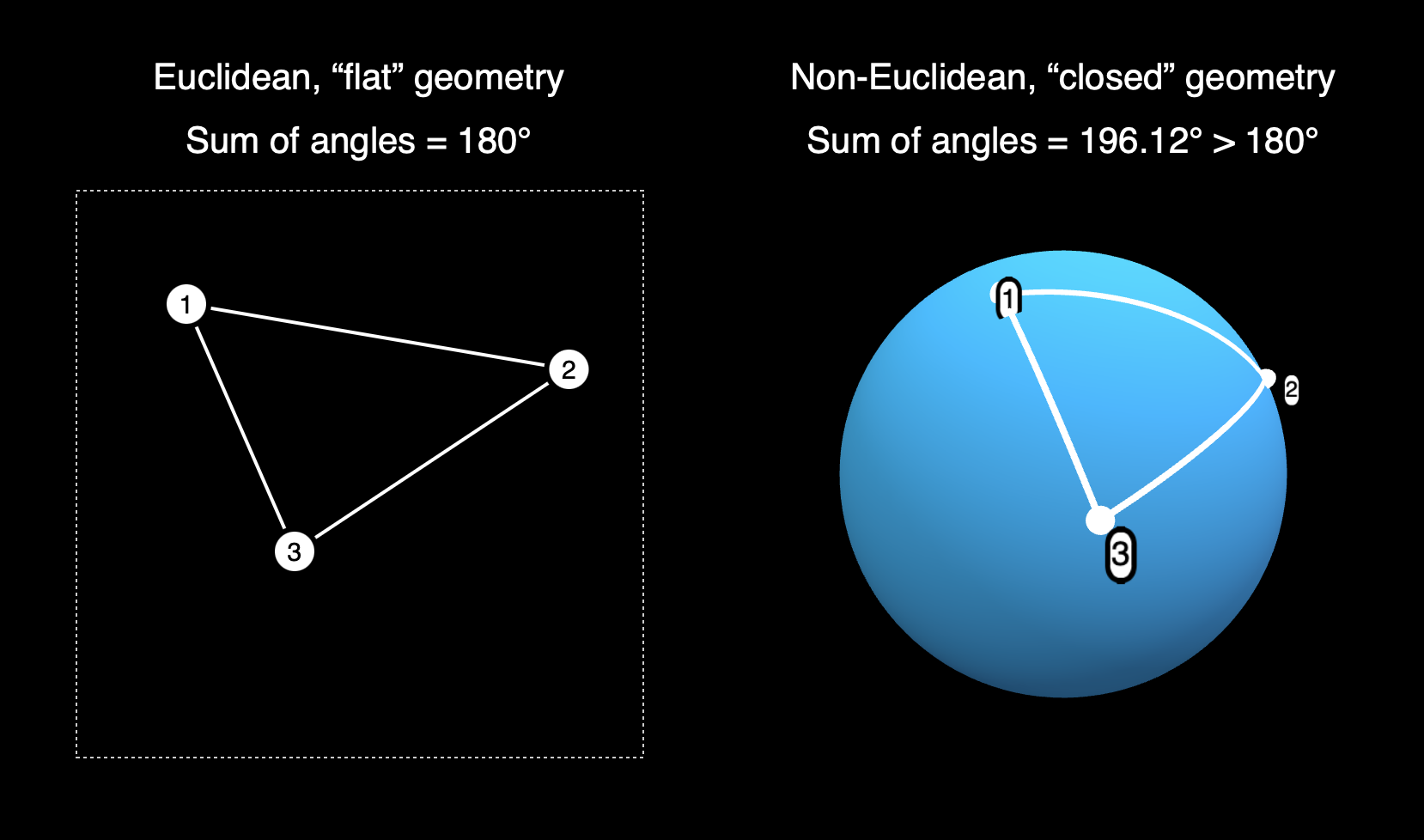
Yes, there are hundreds of Geometry textbooks written and published. What is the reason for this one then? The present lecture notes is written to accompany the course math551, Euclidean and Non-Euclidean Geometries, at UNC Chapel Hill in the early 2000s. The students in this course come from high school and undergraduate education focusing on.. The negatively curved non-Euclidean geometry is called hyperbolic geometry. Euclidean geometry in this classification is parabolic geometry, though the name is less-often used. Spherical geometry is called elliptic geometry, but the space of elliptic geometry is really has points = antipodal pairs on the sphere. With this idea, two lines really
4.3 NonEuclidean Geometry World Science U

A Simple NonEuclidean Geometry and its Physical BasisYaglom

Euclidean Vs. NonEuclidean Geometry by sophia.shedore

NonEuclidean Geometry YouTube

Solved Greenberg Euclidean and NonEuclidean Geometries,

(PDF) Euclidean and NonEuclidean Geometry Shuvadip Ganguli Academia.edu

7 euclidean&non euclidean geometry

PPT LECTURE 8 PowerPoint Presentation, free download ID669884

PPT NonEuclidean geometry and consistency PowerPoint Presentation, free download ID2683826

PPT Euclidean and NonEuclidean geometries, November 25 PowerPoint Presentation ID3981663

what does Non Euclidean geometry mean?? YouTube

Non Euclidean Geometry Shapes
PPT NonEuclidian Geometry PowerPoint Presentation, free download ID6493990

Euclidean & NonEuclidean Geometries Development and History by Marvin Jay Greenberg

PPT NonEuclidean Geometry PowerPoint Presentation, free download ID2040432

NonEuclidean Geometry (illustrated) (ebook), Henry P. Manning 1230000138550 Boeken

PPT Euclidean and NonEuclidean geometries, November 25 PowerPoint Presentation ID3981663

NonEuclidean geometry YouTube

PPT NonEuclidean Geometry PowerPoint Presentation, free download ID2040432

EUCLIDEAN AND NONEUCLIDEAN GEOMETRIES DEVELOPMENT AND HISTORY written by Greenberg, Marvin Jay
Non-Euclidean geometries showed that different systems of geometry could be developed, depending on the assumptions or axioms that were used. The choice of axioms was not a matter of absolute truth but rather a matter of convention or convenience. Therefore, although the axiomatic method was a powerful tool for organizing and systematizing.. non-Euclidean geometry was logically consistent. This problem was not solved until 1870, when Felix Klein (1849-1925) developed an \analytic" description of this geometry. In Klein's description, a \point" of the Gauss-Bolyai-Lobachevsky (G-B-L) geometry can be described by two real number coordinates (x,y), with the restriction x2 + y2 <1.