Equazione Retta passante per due Punti esercizio 5 YouTube

Ora vogliamo capire come possiamo scrivere l' EQUAZIONE della RETTA passante per DUE PUNTI. Immaginiamo di avere i punti. P 0 (x 0 ; y 0) e P 1 (x 1 ; y 1) e di voler scrivere la retta passante per essi. Iniziamo con lo scrivere il FASCIO di RETTE passanti per P 0. Essa è. y - y 0 = m (x - x 0).. L' equazione di una retta passante per due punti distinti (x1,y1) ( x 1, y 1) e (x2,y2) ( x 2, y 2) del piano può essere trovata utilizzando la formula seguente: y −y1 y2 − y1 = x− x1 x2 − x1 y − y 1 y 2 − y 1 = x − x 1 x 2 − x 1. Questa formula è anche detta " condizione di allineamento della retta ". Permette di ottenere l' equazione della retta.

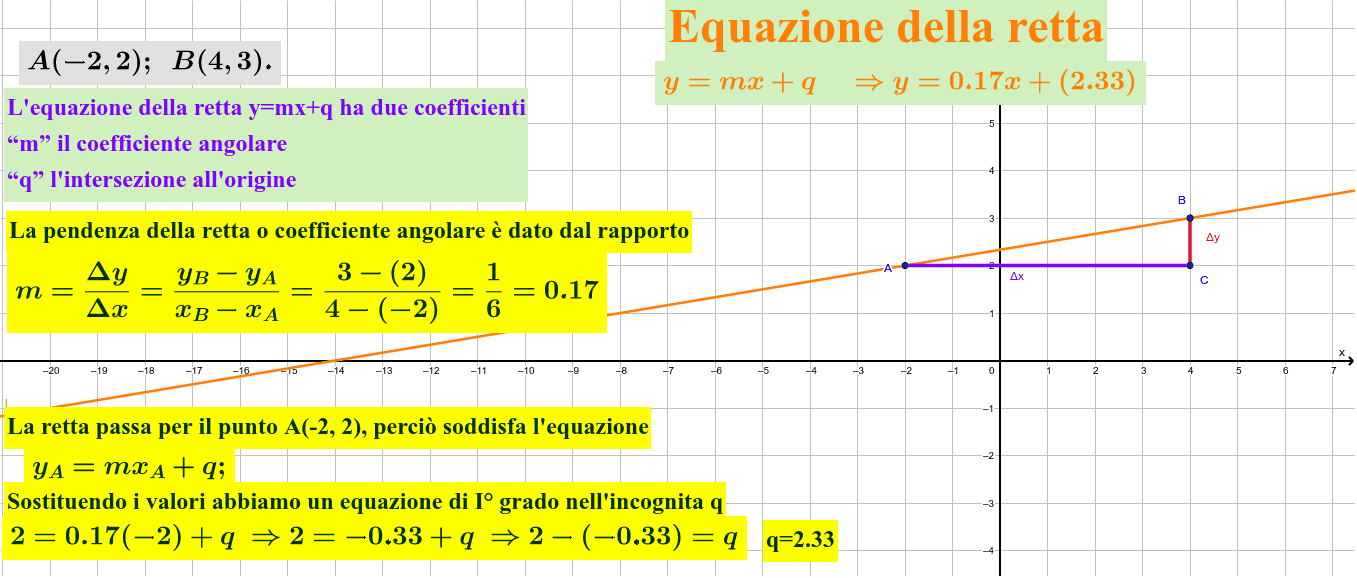
Equazione Di Una Retta Dati Due Punti camhakir

Equazione di una retta per due punti. Matematica terza media

Il piano cartesiano e la retta Mappe schemi

Piano cartesiano e retta Bergamini Barozzi Trifone La

La retta passante per uno e due punti Andrea il Matematico

Equazione della retta passante per un punto matematicaoggi

Equazione Retta passante per due Punti esercizio 5 YouTube

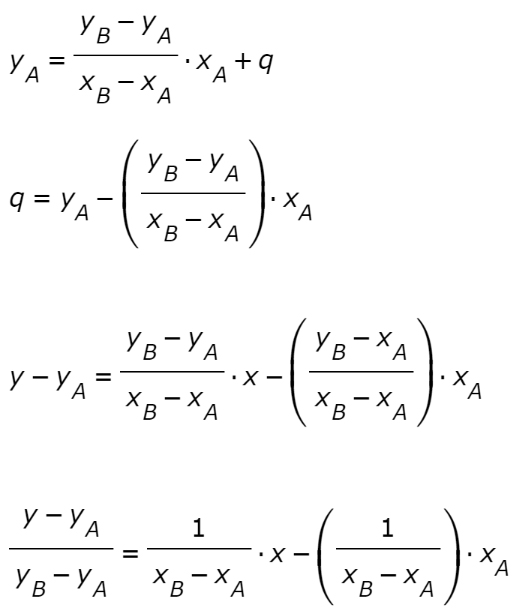
Retta passante per due punti la formula completa con esercizi svolti

EQUAZIONE GENERALE DELLA RETTA lezioniignoranti

Equazione della retta per due punti YouTube

Equazione Della Retta Passante Per Un Punto ignayler

La retta passante per uno e due punti Andrea il Matematico

Equazione Retta passante per 2 punti Esercizio 1 YouTube

Equazione della Retta Passante per Due Punti YouTube

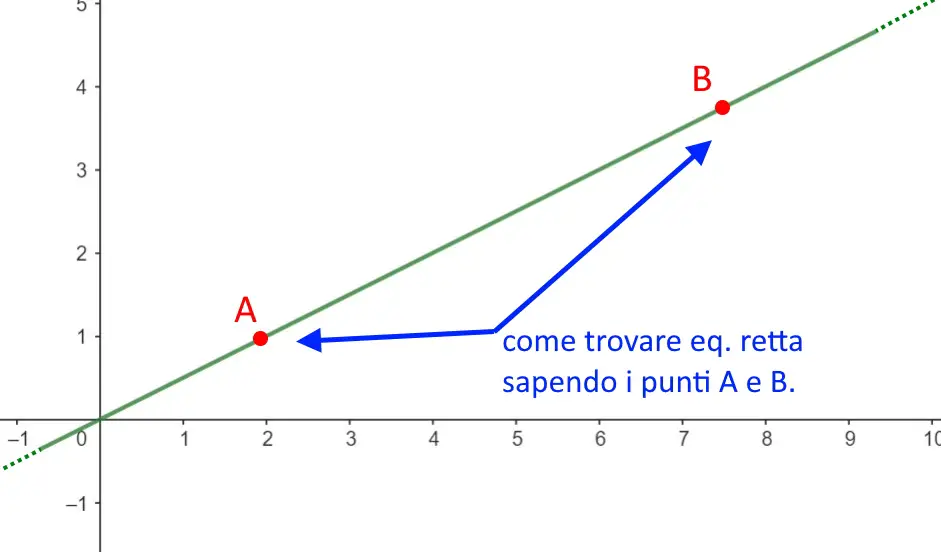
Come trovare l'equazione della retta ESEMPI MondoFisica

Equazione retta passante per due punti formula per coefficiente angolare e fascio proprio YouTube

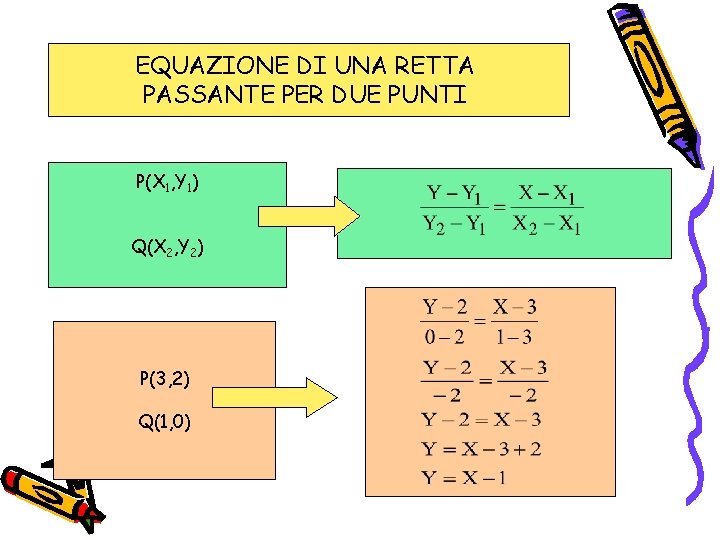
Il piano cartesiano e la retta Mappe schemi

EQUAZIONE della RETTA per due PUNTI _ PC57 YouTube

Funzione lineare, equazione della retta, definizione di coefficiente angolare, fascio di rette, equazione di una retta passante per due punti, condizione di parallelismo tra due rette, condizione di perpendicolarità tra due rette, lunghezza di un segmento, punto medio di un segmento.. Dopo aver visto, nella lezione precedente, qual è l' EQUAZIONE DELLA RETTA passante per DUE PUNTI, in questa lezione vogliamo vedere alcune applicazioni pratiche. Esempio 1: Scrivere l'equazione della retta passante per i punti. P0 (1 ; -1) e P1 (3 ; 5). Applichiamo la formula: Sappiamo che: x0 = 1. y0 = -1. x1 = 3. y1 = 5.