El cálculo integral es una importante herramienta matemática para resolver problemas físicos, biológicos, financieros, etc. Se utiliza para calcular integrales de funciones complejas, predecir el comportamiento de sistemas físicos, estudiar el movimiento de cuerpos celestes y mucho más. Esta disciplina matemática nos ayuda a entender mejor el mundo y nuestro lugar en él.. Teoría se interpreta como el área bajo la curva de f, entre a y b.Dada una función de una variable real y un intervalo [,] de la recta real, la integral es igual al área de la región del plano limitada entre la gráfica de , el eje , y las líneas verticales = y =, donde son negativas las áreas por debajo del eje . ()El vocablo «integral» también puede hacer referencia a la noción de.

CALCULO INTEGRAL INTEGRALES INMEDIATAS Y DEFINICIÓN DE INTEGRAL DE UNA FUNCION

Integral por partes con teorema fundamental del cálculo integral YouTube

Teoremas Fundamentales Del Calculo Integral Integral Objetos matemáticos

Geometría analítica y álgebra Cálculo integral

3110 Segundo Teorema Fundamental Del Calculo Integral

CÁLCULO INTEGRAL FASE 1
Calculo integral

Aprende CÁLCULO INTEGRAL al estilo MATH ROCKS

INTEGRAL DEFINIDA Ejercicio 8 YouTube

Tabla de Integrales Ejemplos resueltos Yo Soy Tu Profe

Completando el diferencial (Metodo para calculo integral) YouTube

13 Cálculo Integral │Teorema Fundamental del Cálculo (Parte I). YouTube

Curso completo de Cálculo Integral YouTube

INTEGRALES INMEDIATAS. Aprende cálculo integral.
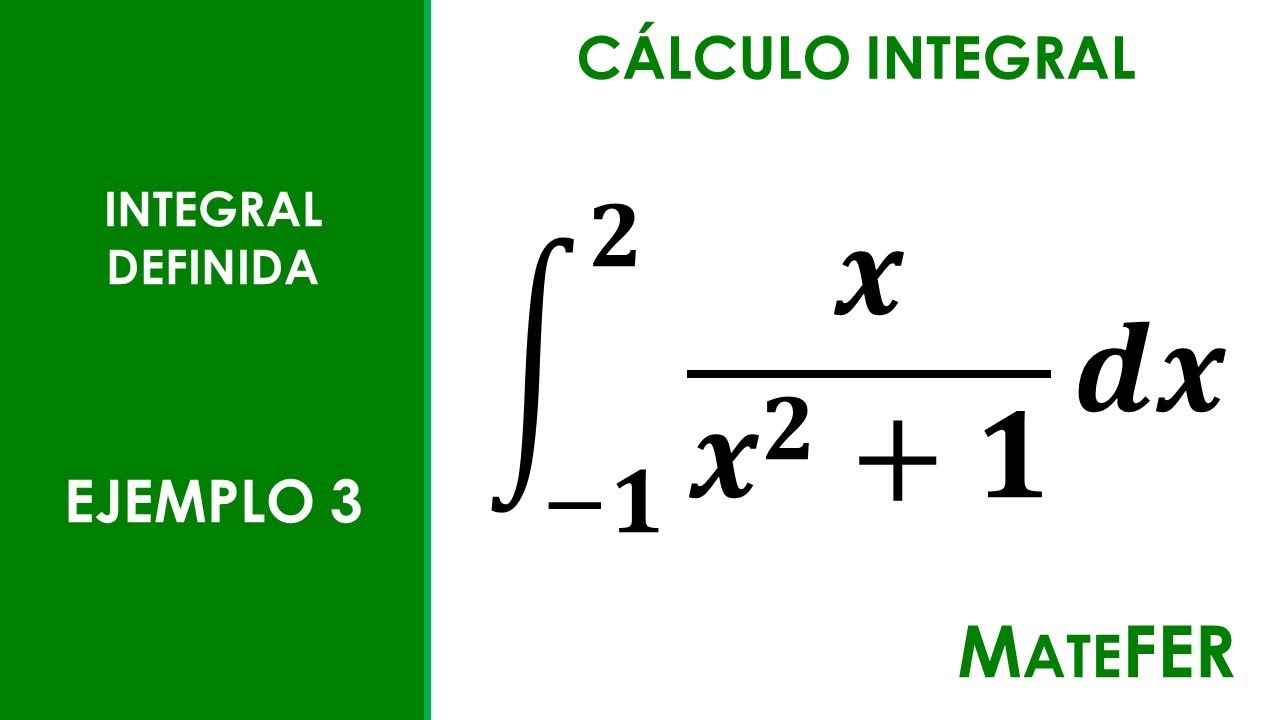
Cálculo Integral Integral Definida EJEMPLO 3 YouTube

PRIMER TEOREMA DE FUNDAMENTAL DEL CÁLCULO INTEGRAL YouTube

Cálculo Integral Constante de Integración EJEMPLO 1 YouTube

Derivando a Integral Aula 3.3 Cálculo Integral YouTube

Cálculo integral Integrales indefinidas Ejercicio 3 YouTube

CALCULO INTEGRAL DEFINIDA Integral Área
Se llama función integral indefinida de la función f al conjunto de todas sus funciones primitivas y se representa como. ∫ f ( x) d x = F ( x) + C. siendo F ( x) una función primitiva de f ( x) y C una constante arbitraria. Ejemplo. La integral indefinida de f ( x) = 2 x es. ∫ 2 x d x = x 2 + C.. El cálculo se divide en dos ramas principales:. Por otro lado, el cálculo integral se basa en el concepto de integral, que se utiliza para calcular el área bajo una curva o el volumen de un sólido. La integral se puede ver como una suma infinita de infinitesimales, lo que permite calcular el área o el volumen de formas irregulares.